 对应
对应
 点的坐标是
点的坐标是
 ,则
,则
 的共轭复数
的共轭复数
 (________ )
(________ ) 满足
满足
 ,则
,则
 (________ )
(________ )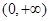 上单调递增的是(________ )
上单调递增的是(________ ) 的展开式中
的展开式中
 的系数为(________ ).
的系数为(________ ). 的焦点为
的焦点为
 ,点
,点
 在
在
 上.若
上.若
 到直线
到直线
 的距离为5,则
的距离为5,则
 (________ )
(________ ) 中,
中,
 ,则
,则
 (________ )
(________ ) ,则“
,则“
 ”是“
”是“
 ”的(________ )
”的(________ ) ,且等腰梯形所在的平面、等腰三角形所在的平面与平面
,且等腰梯形所在的平面、等腰三角形所在的平面与平面
 的夹角的正切值均为
的夹角的正切值均为
 ,则该五面体的所有棱长之和为(________ )
,则该五面体的所有棱长之和为(________ )
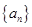 满足
满足
 ,则(________ )
,则(________ ) ,则
,则
 ____________.
____________. 和
和
 ,离心率为
,离心率为
 ,则C的方程为____________.
,则C的方程为____________. 若
若
 为第一象限角,且
为第一象限角,且
 ,则
,则
 .能说明p为假命题的一组
.能说明p为假命题的一组
 的值为
的值为
 __________,
__________,
 _________.
_________.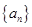 ,该数列的前3项成等差数列,后7项成等比数列,且
,该数列的前3项成等差数列,后7项成等比数列,且
 ,则
,则
 ___________;数列
___________;数列
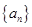 所有项的和为____________.
所有项的和为____________. ,函数
,函数
 ,给出下列四个结论:
,给出下列四个结论: 在区间
在区间
 上单调递减;
上单调递减; 时,
时,
 存在最大值;
存在最大值; ,则
,则
 ;
; .若
.若
 存在最小值,则a的取值范围是
存在最小值,则a的取值范围是
 .
. 中,
中,
 平面
平面
 ,
,
 .
.
 平面PAB;
平面PAB; 的大小.
的大小. .
. ,求
,求
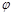 的值.
的值. 在区间
在区间
 上单调递增,
上单调递增,
 ,再从条件①、条件②、条件③这三个条件中选择一个作为已知,使函数
,再从条件①、条件②、条件③这三个条件中选择一个作为已知,使函数
 存在,求
存在,求
 的值.
的值. ;
; ;
; 在区间
在区间
 上单调递减.
上单调递减. 的离心率为
的离心率为
 ,A、C分别是E的上、下顶点,B,D分别是
,A、C分别是E的上、下顶点,B,D分别是
 的左、右顶点,
的左、右顶点,
 .
. 的方程;
的方程; 为第一象限内E上的动点,直线
为第一象限内E上的动点,直线
 与直线
与直线
 交于点
交于点
 ,直线
,直线
 与直线
与直线
 交于点
交于点
 .求证:
.求证:
 .
. ,曲线
,曲线
 在点
在点
 处的切线方程为
处的切线方程为
 .
. 的值;
的值;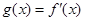 ,求
,求
 的单调区间;
的单调区间; 的极值点个数.
的极值点个数. 的项数均为m
的项数均为m
 ,且
,且

 的前n项和分别为
的前n项和分别为
 ,并规定
,并规定
 .对于
.对于
 ,定义
,定义
 ,其中,
,其中,
 表示数集M中最大的数.
表示数集M中最大的数.  ,求
,求
 的值;
的值; ,且
,且
 ,求
,求
 ;
; ,满足
,满足
 使得
使得
 .
.
暂无任何记录